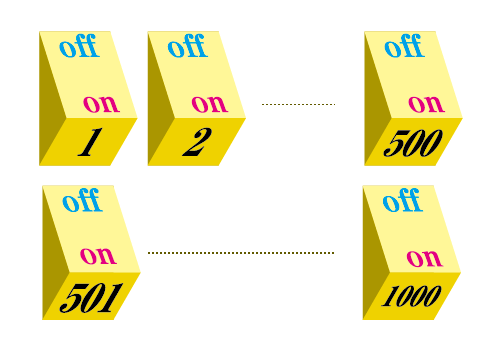
問 スイッチ切り替え問題
ここに1000個のスイッチがあります。全てのスイッチには1番から1000番までの番号が順に振られていて、初めはOFFとなっています。
では、次の試行を繰り返す場合、最終的にONになっているスイッチはいくつあるでしょうか。
・1の倍数のスイッチを切り替える(ONをOFFに、OFFをONにする)
・2の倍数のスイッチを切り替える
・3の倍数のスイッチを切り替える
…
・999の倍数のスイッチを切り替える
・1000の倍数のスイッチを切り替える
答 ONになるスイッチは31個
例えば、6番のスイッチはどうなるのか考えてみましょう。
1回目の試行では、全てのスイッチが切り替わるので、6番スイッチもOFFになります。6は2の倍数なので、2回目の試行でも、切り替わり、3回目の試行でも、切り替わり、OFFになります。ここまでくると気がつきましたか?
ある倍数のスイッチのON・OFFを切り替えるということは、
ON・OFFの切り替え回数
=その数字が持つ1000までの約数の数
ということになります。
6の約数は1・2・3・6の4つ(偶数個)なので、OFFとなります。各スイッチの最終的なON・OFFは、「その番数の持つ約数が偶数個か奇数個か」で決まる、ということが分かります。
すなわち、最終的にONとなるスイッチの番号は、約数が奇数個あるもの、そう、平方数のスイッチとなるのです!
以上より、ONとなるスイッチは、1、4、9、16と続き31×31までの31個と導かれます。
「部分から全体を攻めよ!」
この問題を解くカギとなる論理的な頭の使い方は、「部分から全体を攻めよ!」です。難解な問題を解く際に、まずは小さなモデルを検証すると、解答がスムーズに進みます。
今回であれば、1000個のスイッチ全体の動きを把握しようとするのは大変難しいことです。1つのスイッチ=小さなモデルに絞って検証することで解答のヒントが導きだされました。
「どのような数がON・OFFになるのだろう」と1000個のスイッチに対してぼんやりと思考を巡らせるのではなく、「例えば、6番のスイッチはどうなるのだろう」と具体的な部分に思考を巡らすのです。そうすれば、問題に隠された法則を発見することができます!
これ、本当に数学ではよく使う技術なので、ぜひ使ってみて下さい。
まとめ
きっと受験勉強にも通じる頭の使い方を学べていただけたのではないでしょうか。この論理問題を通じて、頭を使う楽しさを感じてもらえたならとても嬉しいです。
他にも、