はじめに
三角関数の半角公式は、三角関数を扱う上でとても重要な公式です。
単に半角の三角関数の値を求めるだけでなく、次元を落とすために使われるなど、使われる場面が多い公式です。
今回は、半角公式を初めて学習する人や復習したい人に向けて、公式の覚え方、証明の方法、さらに問題の解説を丁寧に行います。
ぜひ最後まで読んで、半角を完璧にマスターしましょう!
目次
半角の公式
まずは半角の公式を確認しましょう。他の公式に比べて形が変わっていて、使いこなすのは大変そうに見えるかもしれません。
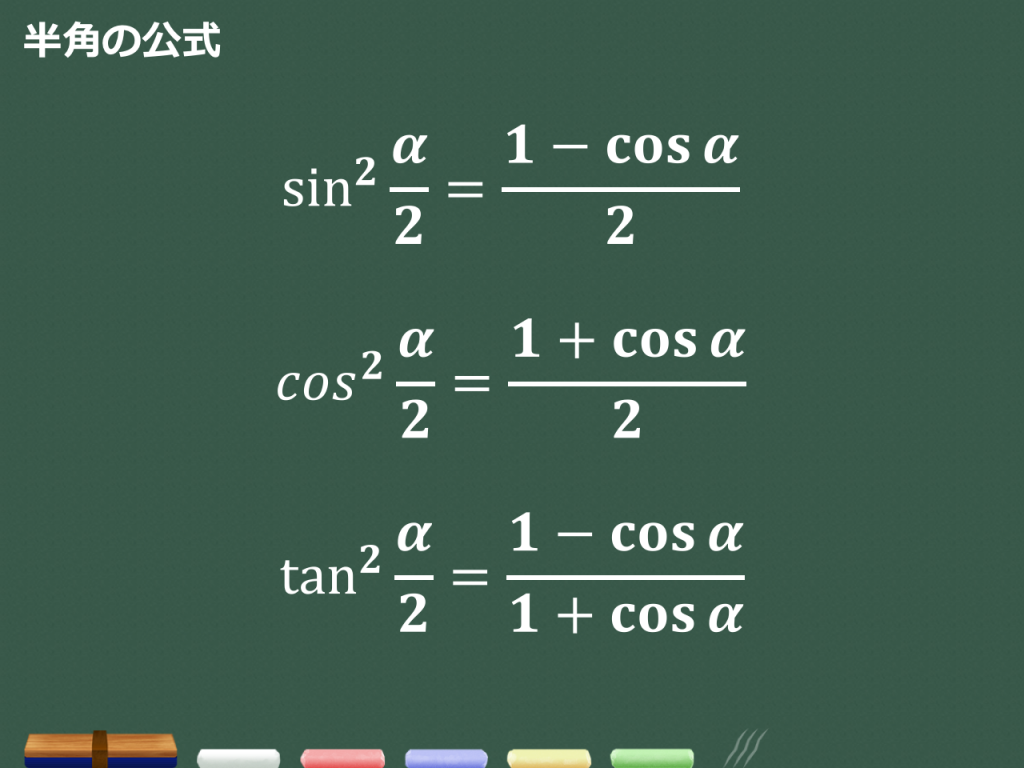
半角の公式の覚え方(語呂合わせ)
三角関数は覚える公式が多いので、少しでも覚える公式を減らしたいですよね。
しかしみなさん、安心して下さい。半角の公式のうち、覚える必要があるのはsinだけです。
\(sin^2\frac{θ}{2}=\frac{1-cosθ}{2}\)
は
「シンジ君は2階に引っ越す」
と覚えましょう。「引っ越す」が「-cosθ」を表しています。
sin以外の半角の公式を覚えるポイント
他の公式を覚えなくていい理由は、sinの式を使って簡単に導けるからです。
cosの半角公式は\(sin^2θ+cos^2θ=1\)に注目して導きましょう。
この性質があることより、半角の場合であっても当然、
\(\sin^2\frac{θ}{2}+\cos^2\frac{θ}{2}=1\)が成り立ちます。
よって
1-(sinの半角公式)
を計算することで、すぐにcosの半角公式が導けるのです。
実際やってみると、
\(1-\frac{1-\cosθ}{2}=\frac{1+\cosθ}{2}\)
となり、確かにcosの場合も簡単に導けました。
また、tanも
\(\tanθ=\frac{\sinθ}{\cosθ}\)
を利用することで導くことができます。
これらの性質を利用して、まずは公式を覚えてしまいましょう。
半角の公式の証明をわかりやすく解説
公式を覚えたところで、証明を確認していきましょう。
証明といっても、難しく考える必要はありません。加法定理、倍角の公式を利用するだけで証明できます。
「加法定理ってなんだっけ」「倍角の公式覚えてないや……」という人は、以下の記事で確認しましょう!
sinの半角公式の証明
2倍角の公式より
\(cos2θ=1-2sin^2θ\)
ここで、\(θを\frac{θ}{2}\)に置き換えると
\(cosθ=1-2sin^2\frac{θ}{2}\)
左辺が\(sin^2\frac{θ}{2} \)だけになるように整理すると
\(sin^2\frac{θ}{2}=\frac{1-cosθ}{2} \)
となります。以上で示すことができました。
次はcosです。
cosの半角公式の証明
同様にcosの半角の公式も証明します。
2倍角の公式より
\(cos2θ=2cos^2θ-1\)
が成り立ちます。
ここで、\(θを\frac{θ}{2}\)に置き換えると
\(cosθ=2cos^2\frac{θ}{2}-1\)
となります。
これを左辺が\(cos^2\frac{θ}{2} \)だけになるように整理すると
\(cos^2\frac{θ}{2}=\frac{1+cosθ}{2} \)
となります。よってcosの半角公式も証明することができました。
tanの半角公式の証明
\begin{align}
tan^2\frac{θ}{2}&=\frac{sin^2\frac{θ}{2}}{cos^2\frac{θ}{2}} \\
&=\frac{\frac{1-cosθ}{2}}{\frac{1+cosθ}{2}} \\
&=\frac{1-cosθ}{1+cosθ} \\ \end{align}
tanは解説を入れる隙もなく証明が終わってしまいましたね(笑)
半角の公式の証明のポイント
半角公式の証明のポイントを端的に表すと、
cosの倍角の公式に\(\frac{θ}{2}\)を代入することです。
そうすると、後は式を整理することで証明できます。
また、tanは\(\frac{sinθ}{cosθ}\)から導くことができます。
これらのポイントを覚えておけば、証明は怖くありませんね。
半角の公式の使い方をわかりやすく解説
公式を覚えて証明を学んだところで、実際に問題を解いてみましょう。
問題
$$ π<θ<2π,\\
\cosθ=\frac{1}{3}$$のとき
$$\cos\frac{θ}{2}$$の値を求めよ。
解答
cosθの値がわかっているので早速公式を適用していきます。
\begin{align}
\cos^2\frac{θ}{2}&=\frac{1+\cosθ}{2}\\
&=\frac{1+\frac{1}{3}}{2} \\
&=\frac{2}{3}
\end{align}
これで\(cos^2\frac{θ}{2}\)の値は求まりました。
しかし、すぐに答えを求めることはできません。
θの値によって\(\cos\frac{θ}{2}\)の正負が異なるからです。
よって、次は正負の検討を行います。
問題文の条件にこのようなものがありました。
\(π<θ<2π \)
これより、
\(\frac{π}{2}<\frac{θ}{2}<π\)
となります。問題文の条件から\(\frac{θ}{2}\)の範囲を導くことができました。
これより以下のことが導けます。
\(\cos\frac{θ}{2}<0\)
\(\frac{π}{2}<\frac{θ}{2}<π\)の間で\(cos\frac{θ}{2}\)が正となることはありませんからね。
よって、\(\cos^2\frac{θ}{2}=\frac{2}{3}\)より
\begin{align}
\cos\frac{θ}{2}&=-\sqrt{\frac{2}{3}} \\
&=-\frac{\sqrt{6}}{3} ・・・(答)
\end{align}
半角の公式を使う上での注意点
半角公式を利用する上での注意点は2乗を外すときです。
ここは、試験でもよく狙われます。
θの値によって正か負か変わってくるので、忘れずに符号を確認しましょう。
おわりに
半角の公式は分数になって覚えにくいかもしれませんが、倍角の公式から導き出されることを踏まえると簡単に覚えられます。
また、半角の公式を問題で使うときは、「2乗を外すときだけ、正負に注意する」ようにしましょう。
以上のことさえ注意すれば、半角の公式は完璧です!
三角関数の合成についてもこの機会に確認しましょう!